METHODS
 Polystochastic Models, PSM, Polytope Projects, PTP
Polystochastic Models, PSM, Polytope Projects, PTP
Polystochastic models, PSM and the associated polytope projects architecture PTP, are the tools provided by Polystochastic, PS, to study complexity, self-evolvability and smart systems.
Studying processes then processes of processes and so on, PSM characterizes systems emerging when several stochastic processes occurring at different conditioning levels, are capable to interact with each other, resulting in qualitatively new processes and systems. PTP outlines the bio-inspired general architecture, shared by the operational structure of evolutionary devices, the functional organization of organisms as informational and cognitive systems, and the scientific or engineering methods. The 4D polytope (hypercube) illustrates the PTP elements: states S (at level 0, denoted also K0), conditions K (at levels 1, 2 and 3, denoted K1, K2, and K3).
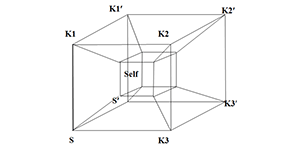
Complementing the synthetic or direct way: S→K1→K2→K3 we need to look at the analytic or dual way: K3’→ K2’ → K1’ → S’.
The central Self coordinates the interaction of the two ways in duality relation.This allow confronting the split between synthesis and analysis and other dichotomies based on the recognition that seemingly contradictory pairs may be more profitably understood as co-equal complementarities rather than exclusive alternatives.Higher dimensional polytopes, 5D, 6D and so on have been considered to face ever growing complexity.
